California Housing - End To End ML Project
ml
In this project, California census data is used to build a model of housing prices in the state. This data includes metrics such as population, median income, and median housing prices for each block in California. Block groups are smallest geographical for which US Census Bureau publishes sample data.
# importing libraries
import numpy as np
import pandas as pd
Get the Data
# get the data
url = 'https://raw.githubusercontent.com/styles3544/handson-ml2/master/datasets/housing/housing.csv'
df = pd.read_csv(url)
df.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | NEAR BAY |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | NEAR BAY |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | NEAR BAY |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | NEAR BAY |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | NEAR BAY |
Quick Analysis of Data
# quick info
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 longitude 20640 non-null float64
1 latitude 20640 non-null float64
2 housing_median_age 20640 non-null float64
3 total_rooms 20640 non-null float64
4 total_bedrooms 20433 non-null float64
5 population 20640 non-null float64
6 households 20640 non-null float64
7 median_income 20640 non-null float64
8 median_house_value 20640 non-null float64
9 ocean_proximity 20640 non-null object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB
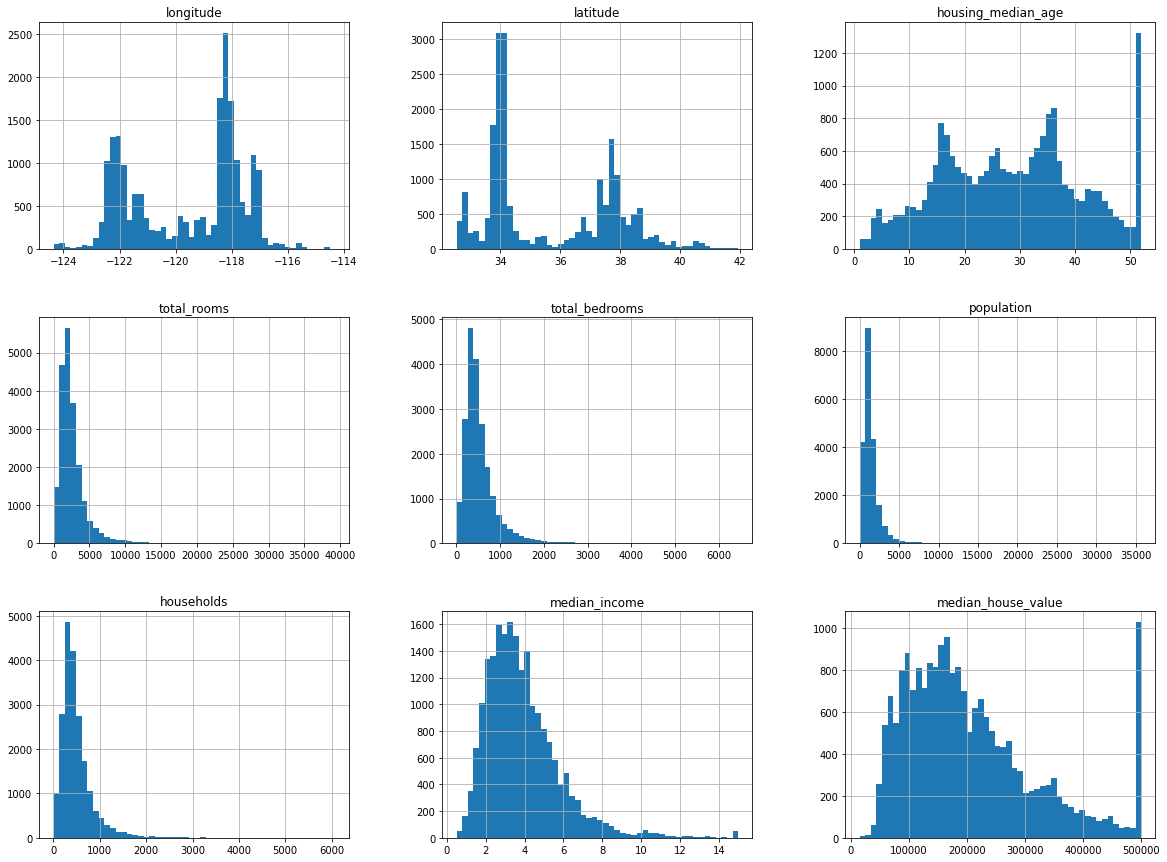
All the attributes are numerical except the ocean_proximity which is an object.
Total instances: 20640
Null values in total_bedrooms
# unique categories present in ocean_proximity column
df['ocean_proximity'].value_counts()
<1H OCEAN 9136
INLAND 6551
NEAR OCEAN 2658
NEAR BAY 2290
ISLAND 5
Name: ocean_proximity, dtype: int64
# summary of numerical attributes
df.describe()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | |
|---|---|---|---|---|---|---|---|---|---|
| count | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20433.000000 | 20640.000000 | 20640.000000 | 20640.000000 | 20640.000000 |
| mean | -119.569704 | 35.631861 | 28.639486 | 2635.763081 | 537.870553 | 1425.476744 | 499.539680 | 3.870671 | 206855.816909 |
| std | 2.003532 | 2.135952 | 12.585558 | 2181.615252 | 421.385070 | 1132.462122 | 382.329753 | 1.899822 | 115395.615874 |
| min | -124.350000 | 32.540000 | 1.000000 | 2.000000 | 1.000000 | 3.000000 | 1.000000 | 0.499900 | 14999.000000 |
| 25% | -121.800000 | 33.930000 | 18.000000 | 1447.750000 | 296.000000 | 787.000000 | 280.000000 | 2.563400 | 119600.000000 |
| 50% | -118.490000 | 34.260000 | 29.000000 | 2127.000000 | 435.000000 | 1166.000000 | 409.000000 | 3.534800 | 179700.000000 |
| 75% | -118.010000 | 37.710000 | 37.000000 | 3148.000000 | 647.000000 | 1725.000000 | 605.000000 | 4.743250 | 264725.000000 |
| max | -114.310000 | 41.950000 | 52.000000 | 39320.000000 | 6445.000000 | 35682.000000 | 6082.000000 | 15.000100 | 500001.000000 |
# plotting histogram for each numerical attribute to get more from the data
import matplotlib.pyplot as plt
%matplotlib inline
df.hist(bins=50, figsize=(20,15))
array([[<matplotlib.axes._subplots.AxesSubplot object at 0x7f947ed6ae50>,
<matplotlib.axes._subplots.AxesSubplot object at 0x7f947ecd1350>,
<matplotlib.axes._subplots.AxesSubplot object at 0x7f947ec87910>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x7f947ec3ef10>,
<matplotlib.axes._subplots.AxesSubplot object at 0x7f947ec01550>,
<matplotlib.axes._subplots.AxesSubplot object at 0x7f947ebb7b50>],
[<matplotlib.axes._subplots.AxesSubplot object at 0x7f947eb78210>,
<matplotlib.axes._subplots.AxesSubplot object at 0x7f947eb2e750>,
<matplotlib.axes._subplots.AxesSubplot object at 0x7f947eb2e790>]],
dtype=object)
Create a Test Set
We are considering random sampling here. It is fine on large dataset but on small dataset, this sampling method may lead to biased results.
For example, when a survey company decides to call 1000 people to ask them questions, they don’t just pick 1000 people randomly from a phone book.
They try to make sure that those 1000 people will represent the entire population. This is called stratified sampling.
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(df, test_size=0.2, random_state=40)
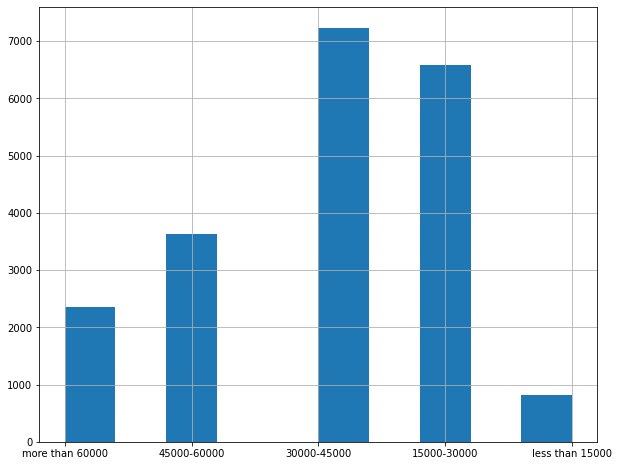
# deriving income category as it should represent the various categories of income in the whole dataset
df['income_category'] = pd.cut(df['median_income'],
bins=[0, 1.5, 3, 4.5, 6, np.inf],
labels=['less than 15000', '15000-30000', '30000-45000', '45000-60000', 'more than 60000'])
# plotting above data
df['income_category'].hist(figsize=(10,8))
<matplotlib.axes._subplots.AxesSubplot at 0x7f946ed88d90>
df['median_income'].value_counts()
3.1250 49
15.0001 49
2.8750 46
4.1250 44
2.6250 44
..
4.1514 1
1.2614 1
2.0294 1
6.7079 1
3.7306 1
Name: median_income, Length: 12928, dtype: int64
df.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | income_category | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -122.23 | 37.88 | 41.0 | 880.0 | 129.0 | 322.0 | 126.0 | 8.3252 | 452600.0 | NEAR BAY | more than 60000 |
| 1 | -122.22 | 37.86 | 21.0 | 7099.0 | 1106.0 | 2401.0 | 1138.0 | 8.3014 | 358500.0 | NEAR BAY | more than 60000 |
| 2 | -122.24 | 37.85 | 52.0 | 1467.0 | 190.0 | 496.0 | 177.0 | 7.2574 | 352100.0 | NEAR BAY | more than 60000 |
| 3 | -122.25 | 37.85 | 52.0 | 1274.0 | 235.0 | 558.0 | 219.0 | 5.6431 | 341300.0 | NEAR BAY | 45000-60000 |
| 4 | -122.25 | 37.85 | 52.0 | 1627.0 | 280.0 | 565.0 | 259.0 | 3.8462 | 342200.0 | NEAR BAY | 30000-45000 |
# doing stratified splitting to represent all category of median_income
strat_X_train, strat_X_test, strat_y_train, strat_y_test = train_test_split(df, df, test_size=0.2, random_state=43, stratify=df['income_category'])
strat_y_test['income_category'].value_counts()/len(strat_y_test)
30000-45000 0.350533
15000-30000 0.318798
45000-60000 0.176357
more than 60000 0.114341
less than 15000 0.039971
Name: income_category, dtype: float64
strat_X_train['income_category'].value_counts()/len(strat_X_train)
30000-45000 0.350594
15000-30000 0.318859
45000-60000 0.176296
more than 60000 0.114462
less than 15000 0.039789
Name: income_category, dtype: float64
As you can see that our training set and test sets are splited in equal proportions of income_category
# now we should remove the income category column from our data to revert the data back to its original form
for strat_set in (strat_X_train, strat_X_test, strat_y_train, strat_y_test):
strat_set.drop(['income_category'], axis=1, inplace=True)
strat_X_train.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 8032 | -118.13 | 33.83 | 44.0 | 1710.0 | 333.0 | 786.0 | 344.0 | 4.2917 | 314700.0 | <1H OCEAN |
| 16031 | -122.45 | 37.72 | 46.0 | 1406.0 | 235.0 | 771.0 | 239.0 | 4.7143 | 219300.0 | NEAR BAY |
| 4108 | -118.37 | 34.13 | 28.0 | 4287.0 | 627.0 | 1498.0 | 615.0 | 8.5677 | 500001.0 | <1H OCEAN |
| 13593 | -117.28 | 34.11 | 39.0 | 1573.0 | 418.0 | 1258.0 | 359.0 | 1.4896 | 69500.0 | INLAND |
| 1100 | -121.75 | 39.88 | 16.0 | 2867.0 | 559.0 | 1203.0 | 449.0 | 2.7143 | 95300.0 | INLAND |
strat_y_test.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 19132 | -122.70 | 38.23 | 47.0 | 2090.0 | 387.0 | 1053.0 | 377.0 | 3.5673 | 310300.0 | <1H OCEAN |
| 20203 | -119.20 | 34.25 | 18.0 | 3208.0 | 643.0 | 1973.0 | 614.0 | 3.8162 | 235000.0 | NEAR OCEAN |
| 13234 | -117.66 | 34.14 | 8.0 | 1692.0 | 253.0 | 857.0 | 251.0 | 6.9418 | 310500.0 | INLAND |
| 5894 | -118.32 | 34.16 | 49.0 | 1074.0 | 170.0 | 403.0 | 208.0 | 6.2547 | 366700.0 | <1H OCEAN |
| 4253 | -118.35 | 34.10 | 18.0 | 7432.0 | 2793.0 | 3596.0 | 2270.0 | 2.8036 | 225000.0 | <1H OCEAN |
Discover and Visualize the Data to Gain Insights
# making a copy so that we don't transform training data
housing = strat_X_train.copy()
# plotting geographical information on scatter plot ---> latitute and longitude
housing.plot(kind='scatter', x='longitude', y='latitude')
<matplotlib.axes._subplots.AxesSubplot at 0x7f946ea921d0>
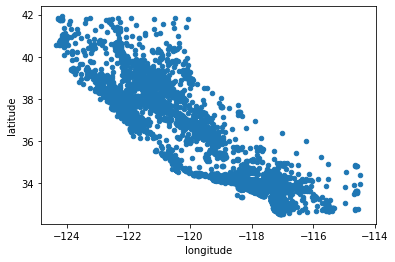
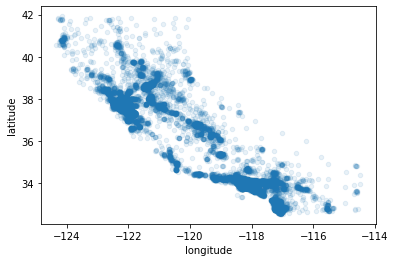
Above plot doesn’t give any information so we will use alpha=0.1 parameter to see the regions where density of the data points is high
housing.plot(kind='scatter', x='longitude', y='latitude', alpha=0.1)
<matplotlib.axes._subplots.AxesSubplot at 0x7f946d78ea90>
housing.plot(kind='scatter', x='longitude', y='latitude', alpha=0.4,
c='median_house_value', cmap=plt.get_cmap("jet"), colorbar=True,
s=housing['population']/100, label='population',
figsize=(10,7));
plt.legend();
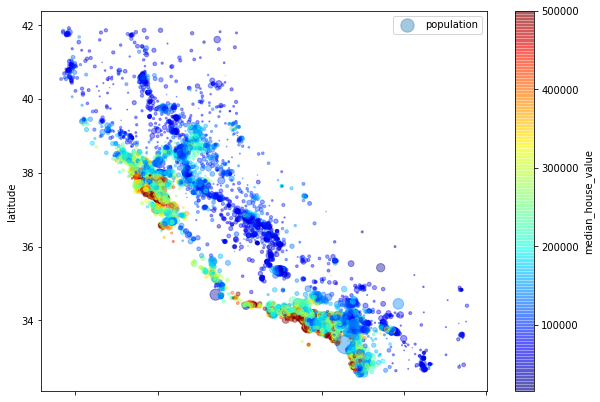
-
As we can see that housing prices depends on the proximity to the ocean and the population density. But in the upper half of the plot the ocean proximity might not be best to describe the prices of house.
-
We can use clustering to find the main clusters and add a feature proximity_from_cluster_center to the dataset. Although, this might not be useful for upper part of the diagram or the North part.
# we can see the correlation of various features with the median housing price
corr_matrix = housing.corr()
# seeing how much each attribute correlates with the median house value
corr_matrix['median_house_value'].sort_values(ascending=False)
median_house_value 1.000000
median_income 0.691068
total_rooms 0.138526
housing_median_age 0.102086
households 0.068405
total_bedrooms 0.052128
population -0.021388
longitude -0.043072
latitude -0.146273
Name: median_house_value, dtype: float64
Observations to make:
- Values range from -1 to 1
- median house value tends to go up when the median income goes up (strong positive correlation)
- prices have tendency to go down when you go north (negative correlation between latitude and median)
Note: The correlation coefficient only measures linear correlations (“if x goes up, then y generally goes up/down”). It may completely miss uot on non-linaer relationship.
housing.columns
Index(['longitude', 'latitude', 'housing_median_age', 'total_rooms',
'total_bedrooms', 'population', 'households', 'median_income',
'median_house_value', 'ocean_proximity'],
dtype='object')
num_cols = [col for col in list(housing.columns)
if housing[col].dtype == 'float64']
num_cols
['longitude',
'latitude',
'housing_median_age',
'total_rooms',
'total_bedrooms',
'population',
'households',
'median_income',
'median_house_value']
# plotting correlation among attributes using pandas
from pandas.plotting import scatter_matrix
scatter_matrix(housing[num_cols], figsize=(20,15));
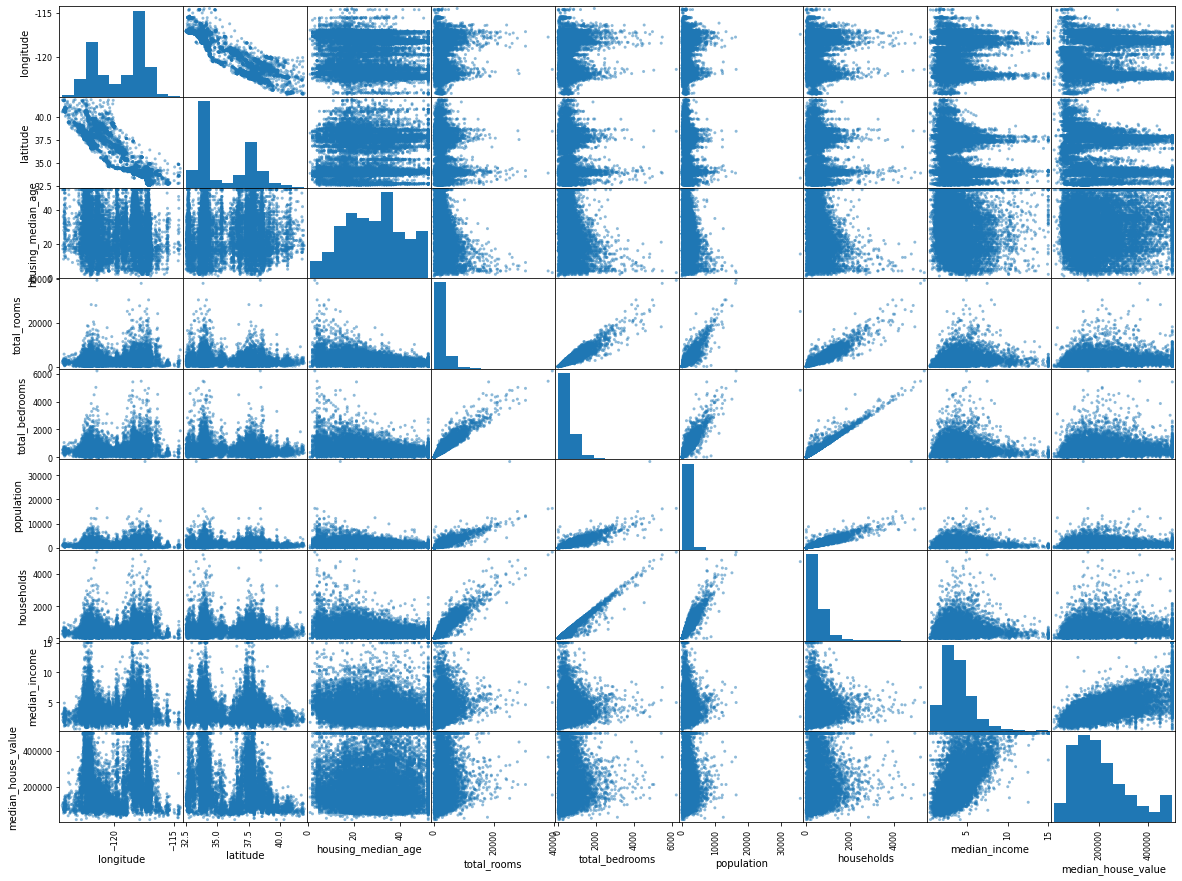
Above scatter matrix plots every numerical attribute against every numerical attribute, plus a histogram of each numerical attribute.
# plotting median_income against median_house_value
housing.plot(kind='scatter', x='median_income', y='median_house_value', alpha=0.1)
<matplotlib.axes._subplots.AxesSubplot at 0x7f946a69ac90>
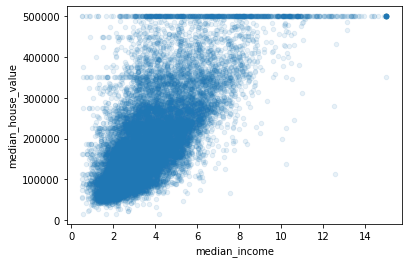
We can clearly see the price cap clearly visible as a line at 500000 and it also reveals some other lines below it. One at around 450000 and at around 350000 and maybe two between 200000 to 300000.
We might wnat to remove these data points in order to avoid our model learning those trends.
Moreover, we can clearly see the correlation between the two variables is very strong. The trend is increasing and the data points are also not very dispersed.
Up till now we observed the following:
- Identified few data quirks that we may want to clean up before feeding the data to ML algorithm.
- Found correlation between attributes with respect to the target.
- Noticed that some attributes have a tail heavy distribution which might need to be transformed.
Combining Attributes and Experimentation
Try out various attribute combinations.
housing.columns
Index(['longitude', 'latitude', 'housing_median_age', 'total_rooms',
'total_bedrooms', 'population', 'households', 'median_income',
'median_house_value', 'ocean_proximity'],
dtype='object')
housing['rooms_per_household'] = housing['total_rooms']/housing['households']
housing['bedrooms_per_room'] = housing['total_bedrooms']/housing['total_rooms']
housing['population_per_household'] = housing['population']/housing['households']
housing.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | rooms_per_household | bedrooms_per_room | population_per_household | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8032 | -118.13 | 33.83 | 44.0 | 1710.0 | 333.0 | 786.0 | 344.0 | 4.2917 | 314700.0 | <1H OCEAN | 4.970930 | 0.194737 | 2.284884 |
| 16031 | -122.45 | 37.72 | 46.0 | 1406.0 | 235.0 | 771.0 | 239.0 | 4.7143 | 219300.0 | NEAR BAY | 5.882845 | 0.167141 | 3.225941 |
| 4108 | -118.37 | 34.13 | 28.0 | 4287.0 | 627.0 | 1498.0 | 615.0 | 8.5677 | 500001.0 | <1H OCEAN | 6.970732 | 0.146256 | 2.435772 |
| 13593 | -117.28 | 34.11 | 39.0 | 1573.0 | 418.0 | 1258.0 | 359.0 | 1.4896 | 69500.0 | INLAND | 4.381616 | 0.265734 | 3.504178 |
| 1100 | -121.75 | 39.88 | 16.0 | 2867.0 | 559.0 | 1203.0 | 449.0 | 2.7143 | 95300.0 | INLAND | 6.385301 | 0.194977 | 2.679287 |
corr_mat = housing.corr()
corr_mat['median_house_value'].sort_values(ascending=False)
median_house_value 1.000000
median_income 0.691068
rooms_per_household 0.181512
total_rooms 0.138526
housing_median_age 0.102086
households 0.068405
total_bedrooms 0.052128
population -0.021388
population_per_household -0.022279
longitude -0.043072
latitude -0.146273
bedrooms_per_room -0.258447
Name: median_house_value, dtype: float64
bedrooms_per_room is much more correlated with median_house_value than total_rooms or total_bedrooms.
Houses with lower bedroom/room ration is expected to be more expensive.
Also, rooms_per_household is more informative than total_rooms having positive correlation which is obvious
Prepare the Data for Machine Learning Algorithm
Make a clean training set by copying strat_X_train once again. We also need to drop the predictor and target variables. We can do this by drop() as it creates the copy of the original without disturbing the original dataset.
housing = strat_X_train.drop('median_house_value', axis=1)
housing_labels = strat_X_train['median_house_value'].copy()
Data Cleaning
We have three ways to do this:
- Dropping all rows with null values
- Dropping all columns with null values
- Imputations
housing.isnull().sum()
longitude 0
latitude 0
housing_median_age 0
total_rooms 0
total_bedrooms 172
population 0
households 0
median_income 0
ocean_proximity 0
dtype: int64
# using sklearn to impute median values
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy='median')
num_colms = [col for col in list(housing.columns)
if housing[col].dtype == 'float64']
num_colms
['longitude',
'latitude',
'housing_median_age',
'total_rooms',
'total_bedrooms',
'population',
'households',
'median_income']
imputed = imputer.fit_transform(housing[num_colms])
imputed
array([[-1.1813e+02, 3.3830e+01, 4.4000e+01, ..., 7.8600e+02,
3.4400e+02, 4.2917e+00],
[-1.2245e+02, 3.7720e+01, 4.6000e+01, ..., 7.7100e+02,
2.3900e+02, 4.7143e+00],
[-1.1837e+02, 3.4130e+01, 2.8000e+01, ..., 1.4980e+03,
6.1500e+02, 8.5677e+00],
...,
[-1.2132e+02, 3.8630e+01, 2.0000e+01, ..., 3.1070e+03,
1.3150e+03, 3.0348e+00],
[-1.1783e+02, 3.4150e+01, 2.0000e+01, ..., 1.0230e+03,
2.9800e+02, 8.0683e+00],
[-1.1801e+02, 3.4090e+01, 3.2000e+01, ..., 1.2830e+03,
4.0400e+02, 3.1944e+00]])
# converting to data frame
housing_tr = pd.DataFrame(
imputed,
columns = housing[num_colms].columns,
index = housing[num_colms].index
)
housing_tr.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | |
|---|---|---|---|---|---|---|---|---|
| 8032 | -118.13 | 33.83 | 44.0 | 1710.0 | 333.0 | 786.0 | 344.0 | 4.2917 |
| 16031 | -122.45 | 37.72 | 46.0 | 1406.0 | 235.0 | 771.0 | 239.0 | 4.7143 |
| 4108 | -118.37 | 34.13 | 28.0 | 4287.0 | 627.0 | 1498.0 | 615.0 | 8.5677 |
| 13593 | -117.28 | 34.11 | 39.0 | 1573.0 | 418.0 | 1258.0 | 359.0 | 1.4896 |
| 1100 | -121.75 | 39.88 | 16.0 | 2867.0 | 559.0 | 1203.0 | 449.0 | 2.7143 |
housing_tr.isnull().sum()
longitude 0
latitude 0
housing_median_age 0
total_rooms 0
total_bedrooms 0
population 0
households 0
median_income 0
dtype: int64
We don’t have any missing values now.
#Handling Text and Categorical Values
housing_cat = housing['ocean_proximity']
housing_cat.head(10)
8032 <1H OCEAN
16031 NEAR BAY
4108 <1H OCEAN
13593 INLAND
1100 INLAND
18953 INLAND
8759 NEAR OCEAN
2282 INLAND
2233 INLAND
15262 NEAR OCEAN
Name: ocean_proximity, dtype: object
# converting category into numbers using ordinal encoder
from sklearn.preprocessing import OrdinalEncoder
oe = OrdinalEncoder()
housing_cat_encoded = oe.fit_transform(np.array(housing_cat).reshape(-1,1))
housing_cat_encoded[:10]
array([[0.],
[3.],
[0.],
[1.],
[1.],
[1.],
[4.],
[1.],
[1.],
[4.]])
oe.categories_
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]
This representaion has an issue with the ML algorithm, i.e., ML algorithm will assume two nearby values to be more similar than two distant values. It is fine in the case of ordinal data where order matters but not in this case.
So, we’ll do one hot encoding.
# onehot encoding
from sklearn.preprocessing import OneHotEncoder
onehot = OneHotEncoder()
housing_cat_onehot_encoded = onehot.fit_transform(np.array(housing_cat).reshape(-1,1))
housing_cat_onehot_encoded
<16512x5 sparse matrix of type '<class 'numpy.float64'>'
with 16512 stored elements in Compressed Sparse Row format>
housing_cat_onehot_encoded.toarray()
array([[1., 0., 0., 0., 0.],
[0., 0., 0., 1., 0.],
[1., 0., 0., 0., 0.],
...,
[0., 1., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 1., 0., 0., 0.]])
onehot.categories_
[array(['<1H OCEAN', 'INLAND', 'ISLAND', 'NEAR BAY', 'NEAR OCEAN'],
dtype=object)]
If a categorical attribute has large number of possible categories then one hot encoding will result in large number of input features. This may slow down training or degrade performance.
If this happens the you many want to replace the categorical attribute with a numerical feature related to the category.
For Example: ocean_proximity can be replaced with distance_from_ocean
This way, you can replace each category with a learnable, low dimentional vector called an embedding.
Each categories representation would be learned during training. This is an example of representation learning.
Transformation Pipelines
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
numerical_pipeline = Pipeline(
steps = [
('imputer', SimpleImputer(strategy='median')),
('scalar', StandardScaler())
]
)
# making a pipeline which can handle both numerical and categorical data
from sklearn.compose import ColumnTransformer
cat_colms = ['ocean_proximity']
full_pipeline = ColumnTransformer(
transformers=[
('numpipe', numerical_pipeline, num_colms),
('cat', OneHotEncoder(), cat_colms)
]
)
housing_transformed = full_pipeline.fit_transform(housing)
housing_transformed
array([[ 0.72296892, -0.84564688, 1.21573919, ..., 0. ,
0. , 0. ],
[-1.4316449 , 0.97476553, 1.3749774 , ..., 0. ,
1. , 0. ],
[ 0.60326815, -0.70525518, -0.0581665 , ..., 0. ,
0. , 0. ],
...,
[-0.86805379, 1.40062037, -0.69511935, ..., 0. ,
0. , 0. ],
[ 0.87259488, -0.69589573, -0.69511935, ..., 0. ,
0. , 0. ],
[ 0.78281931, -0.72397408, 0.26030992, ..., 0. ,
0. , 0. ]])
housing_transformed.shape
(16512, 13)
housing.shape
(16512, 9)
data_tr = pd.DataFrame(
housing_transformed,
index = housing.index
)
Select and Train a Model
###Training and Evaluating on Training Set
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
reg = LinearRegression()
reg.fit(housing_transformed, housing_labels)
preds = reg.predict(housing_transformed)
lin_mse = mean_squared_error(housing_labels, preds)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
68423.21331810919
Not a great score as mean_housing_value ranges between 120000 to 265000, so prediction erroe of 68423 in not good.
This is an example of model underfitting the training data.
This can mean that the feature do not provide enough information to make good predictions, or the model is not powerful enough.
This can be solved by:
- selecting more powerful model
- feed better training features
- reduce the constraints on the model
# we should save every model so that we can come back to it later
import joblib
#joblib.dump(reg, "reg_model.pkl")
# later we can load by using ---> joblib.load("reg_model.pkl")
# trying decision tree
from sklearn.tree import DecisionTreeRegressor
dt_reg = DecisionTreeRegressor()
dt_reg.fit(housing_transformed, housing_labels)
tree_preds = dt_reg.predict(housing_transformed)
tree_mse = mean_squared_error(housing_labels, tree_preds)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
0.0
This is a clear example of overfitting on the training data. The tree regressor has badly overfitted itself on data.
To make sure above, we evaluate decision tree model using cross-validation.
Better Evaluation Using Cross-Validation
We will split the data into a smaller training set and a validation set, then train our model on small training set and evaluate it on the validation set.
Alternative to above, we can do K-fold cross-validation. In this we randomly split training training set into 10 distinct subsets called folds, then train and evaluate the model 10 times, picking a different fold for evaluation every time and training on the other 9 folds.
The result consists of array having 10 evaluation scores.
from sklearn.model_selection import cross_val_score
scores = cross_val_score(dt_reg, housing_transformed, housing_labels, scoring='neg_mean_squared_error', cv=10)
tree_rmse_scores = np.sqrt(-scores)
def display_scores(scores):
print("Scores: ", scores)
print("Mean: ", scores.mean())
print("Standard deviation: ", scores.std())
display_scores(tree_rmse_scores)
Scores: [71031.79298008 67250.24012972 70704.6010507 71025.7707032
71160.52527914 68667.39830772 68006.08733069 66079.96490705
67688.62231723 70089.57080823]
Mean: 69170.45738137637
Standard deviation: 1763.7611372201977
Now we can see that Decision Tree model didn’t do actually that well. It even did worse than linear regression model.
# saving dt model
#joblib.dump(dt_reg, "decision_tree_reg_model.pkl")
# trying last model ---> Random Forest
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_transformed, housing_labels)
forest_preds = forest_reg.predict(housing_transformed)
forest_mse = mean_squared_error(housing_labels, forest_preds)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
18175.154173733696
# doing cross-validation
forest_scores = cross_val_score(forest_reg ,housing_transformed, housing_labels,
scoring='neg_mean_squared_error',
cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
Scores: [50999.08275972 48680.10166331 49212.61255093 48800.12448082
48193.62916323 50187.14221101 45646.74161486 48421.53480168
47894.28559274 50450.44975909]
Mean: 48848.57045973879
Standard deviation: 1446.354910876353
Random Forest model did even better tha Decision Tree model.
We can try more models like SVM with different kernels and all. But let’s first save the model.
# saving random forest model
#joblib.dump(forest_reg, "rand_forst_reg_model.pkl")
Fine Tune Model
Grid Search
Choosing the best hyperparameters by manually tweaking it is a tedious process. Instead, we can tell GridSearchCV all the parameters that we wnanna use and it’ll find the best one for us.
from sklearn.model_selection import GridSearchCV
# all the parameters we want to use
parameters =[
{'n_estimators': [3, 10, 30, 100, 1000], 'max_features': [2, 4, 6, 8]},
{'bootstrap': [False], 'n_estimators': [3, 10,30, 100, 1000], 'max_features': [2, 3, 4]}
]
# Instance
grid_search = GridSearchCV(forest_reg,
param_grid=parameters,
cv=5,
scoring='neg_mean_squared_error')
grid_search.fit(housing_transformed, housing_labels)
GridSearchCV(cv=5, estimator=RandomForestRegressor(),
param_grid=[{'max_features': [2, 4, 6, 8],
'n_estimators': [3, 10, 30, 100, 1000]},
{'bootstrap': [False], 'max_features': [2, 3, 4],
'n_estimators': [3, 10, 30, 100, 1000]}],
scoring='neg_mean_squared_error')
It took 29m 42s to run the above snippet of code. Thanks to my computer. It’s time to check the best parameters and scores.
np.sqrt(-1*grid_search.best_score_)
48677.93672357493
grid_search.best_params_
{'bootstrap': False, 'max_features': 4, 'n_estimators': 1000}
grid_search.best_estimator_
RandomForestRegressor(bootstrap=False, max_features=4, n_estimators=1000)
# all the evaluation scores
cv_results = grid_search.cv_results_
for mean_score, param in zip(cv_results['mean_test_score'], cv_results['params']):
print(np.sqrt(-mean_score), param)
63574.450259463985 {'max_features': 2, 'n_estimators': 3}
55513.84547975345 {'max_features': 2, 'n_estimators': 10}
52330.134450409794 {'max_features': 2, 'n_estimators': 30}
51482.154385360096 {'max_features': 2, 'n_estimators': 100}
51149.235982557664 {'max_features': 2, 'n_estimators': 1000}
60348.40552124982 {'max_features': 4, 'n_estimators': 3}
52678.579693757325 {'max_features': 4, 'n_estimators': 10}
50506.025436890566 {'max_features': 4, 'n_estimators': 30}
49621.88294637385 {'max_features': 4, 'n_estimators': 100}
49312.286517916975 {'max_features': 4, 'n_estimators': 1000}
58801.1210611655 {'max_features': 6, 'n_estimators': 3}
52394.60314992345 {'max_features': 6, 'n_estimators': 10}
49958.935091347004 {'max_features': 6, 'n_estimators': 30}
49052.7131164614 {'max_features': 6, 'n_estimators': 100}
48794.22948920545 {'max_features': 6, 'n_estimators': 1000}
57032.02733646104 {'max_features': 8, 'n_estimators': 3}
52190.76874669462 {'max_features': 8, 'n_estimators': 10}
49816.116646345035 {'max_features': 8, 'n_estimators': 30}
49024.94581188278 {'max_features': 8, 'n_estimators': 100}
48736.6207334852 {'max_features': 8, 'n_estimators': 1000}
62994.15864585694 {'bootstrap': False, 'max_features': 2, 'n_estimators': 3}
53762.11444492626 {'bootstrap': False, 'max_features': 2, 'n_estimators': 10}
51445.86495095677 {'bootstrap': False, 'max_features': 2, 'n_estimators': 30}
50504.049153836946 {'bootstrap': False, 'max_features': 2, 'n_estimators': 100}
50309.144939739526 {'bootstrap': False, 'max_features': 2, 'n_estimators': 1000}
59952.59996832556 {'bootstrap': False, 'max_features': 3, 'n_estimators': 3}
52186.10319347945 {'bootstrap': False, 'max_features': 3, 'n_estimators': 10}
50369.87125095301 {'bootstrap': False, 'max_features': 3, 'n_estimators': 30}
49355.105131321325 {'bootstrap': False, 'max_features': 3, 'n_estimators': 100}
49199.841482919706 {'bootstrap': False, 'max_features': 3, 'n_estimators': 1000}
58109.74190349157 {'bootstrap': False, 'max_features': 4, 'n_estimators': 3}
51727.504969210124 {'bootstrap': False, 'max_features': 4, 'n_estimators': 10}
49664.840151163095 {'bootstrap': False, 'max_features': 4, 'n_estimators': 30}
48865.95463601565 {'bootstrap': False, 'max_features': 4, 'n_estimators': 100}
48677.93672357493 {'bootstrap': False, 'max_features': 4, 'n_estimators': 1000}
We got slightly better RMSE score than we got earlier by using default parameters i.e., 48848, using parameters as n_estimators = 1000, bootstrap = Flase and max_features = 4.
We can also use Randomized Search instead of Grid Search for the same purpose.
Evaluation on Test Set
strat_X_test.head()
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 19132 | -122.70 | 38.23 | 47.0 | 2090.0 | 387.0 | 1053.0 | 377.0 | 3.5673 | 310300.0 | <1H OCEAN |
| 20203 | -119.20 | 34.25 | 18.0 | 3208.0 | 643.0 | 1973.0 | 614.0 | 3.8162 | 235000.0 | NEAR OCEAN |
| 13234 | -117.66 | 34.14 | 8.0 | 1692.0 | 253.0 | 857.0 | 251.0 | 6.9418 | 310500.0 | INLAND |
| 5894 | -118.32 | 34.16 | 49.0 | 1074.0 | 170.0 | 403.0 | 208.0 | 6.2547 | 366700.0 | <1H OCEAN |
| 4253 | -118.35 | 34.10 | 18.0 | 7432.0 | 2793.0 | 3596.0 | 2270.0 | 2.8036 | 225000.0 | <1H OCEAN |
strat_y_test
| longitude | latitude | housing_median_age | total_rooms | total_bedrooms | population | households | median_income | median_house_value | ocean_proximity | |
|---|---|---|---|---|---|---|---|---|---|---|
| 19132 | -122.70 | 38.23 | 47.0 | 2090.0 | 387.0 | 1053.0 | 377.0 | 3.5673 | 310300.0 | <1H OCEAN |
| 20203 | -119.20 | 34.25 | 18.0 | 3208.0 | 643.0 | 1973.0 | 614.0 | 3.8162 | 235000.0 | NEAR OCEAN |
| 13234 | -117.66 | 34.14 | 8.0 | 1692.0 | 253.0 | 857.0 | 251.0 | 6.9418 | 310500.0 | INLAND |
| 5894 | -118.32 | 34.16 | 49.0 | 1074.0 | 170.0 | 403.0 | 208.0 | 6.2547 | 366700.0 | <1H OCEAN |
| 4253 | -118.35 | 34.10 | 18.0 | 7432.0 | 2793.0 | 3596.0 | 2270.0 | 2.8036 | 225000.0 | <1H OCEAN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 18409 | -121.82 | 37.27 | 16.0 | 2030.0 | 321.0 | 1343.0 | 365.0 | 6.3566 | 279100.0 | <1H OCEAN |
| 17213 | -119.72 | 34.44 | 50.0 | 3265.0 | 509.0 | 1256.0 | 443.0 | 6.3997 | 500001.0 | <1H OCEAN |
| 18054 | -121.97 | 37.25 | 21.0 | 2775.0 | 389.0 | 856.0 | 350.0 | 7.9135 | 496400.0 | <1H OCEAN |
| 1988 | -119.81 | 36.74 | 36.0 | 607.0 | 155.0 | 483.0 | 146.0 | 1.5625 | 47500.0 | INLAND |
| 184 | -122.23 | 37.80 | 52.0 | 1252.0 | 299.0 | 844.0 | 280.0 | 2.3929 | 111900.0 | NEAR BAY |
4128 rows × 10 columns
final_model = grid_search.best_estimator_
X_test = strat_X_test.drop('median_house_value', axis=1)
y_test = strat_y_test['median_house_value'].copy()
X_test_transformed = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_transformed)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse
48203.83159835085
Copying the following code for the confidence interval
# 95% confidence interval for generalization error using scipy.stats.t.interval()
from scipy import stats
confidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,
loc=squared_errors.mean(),
scale=stats.sem(squared_errors)))
array([45836.42112908, 50460.29389135])
# Lastly saving the model or pipeline using joblib
joblib.dump(final_model, "final_model_california_housing.pkl")
['final_model_california_housing.pkl']
Author:
subscribe via RSS